| Max Planck Institute of Molecular Plant Physiology | Matthias Scholz |
| Bioinformatics Group |
Approaches to analyse and interpret biological profile data.
University of Potsdam, Germany. 2006.
Ph.D. thesis
Advances in biotechnologies rapidly increase the number of molecules of a cell which can be observed simultaneously. This includes expression levels of thousands or ten-thousands of genes as well as concentration levels of metabolites or proteins.
Such Profile data, observed at different times or at different experimental conditions (e.g., heat or dry stress), show how the biological experiment is reflected on the molecular level. This information is helpful to understand the molecular behaviour and to identify molecules or combination of molecules that characterise specific biological condition (e.g., disease).
This work shows the potentials of component extraction algorithms to identify the major factors which influenced the observed data. This can be the expected experimental factors such as the time or temperature as well as unexpected factors such as technical artefacts or even unknown biological behaviour.
The full text PDF version is available at: URN: urn:nbn:de:kobv:517-opus-7839 and URL: http://opus.kobv.de/ubp/volltexte/2006/783/
Figures of this thesis

The figures are licensed under a
Creative Commons Attribution 2.0 Germany License.
When you use these figures in talks or for teaching etc.,
please acknowledge by reference.
Data visualisation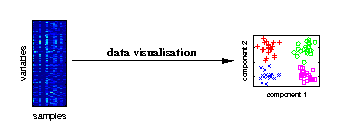
[ pdf | gif | png | eps ] |
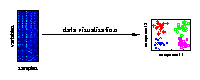
Visualising the major characteristics of high-dimensional data is helpful to understand how molecular data reflect the investigated experimental conditions. The large number of variables is given by genes, metabolites or proteins measured for different biological samples. On the right, a visualisation of samples from different experimental conditions is illustrated. |
Linear and nonlinear components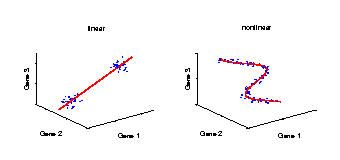
[ pdf | gif | png | eps ] |
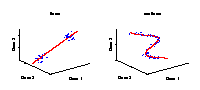
Illustration of a linear and a nonlinear component in a data space. The axes represent the variables (e.g., genes) and the data (blue dots) stand for individual samples from an experiment. A component explains the structure of the data by a straight line in the linear case, or by a curve in the nonlinear case. Linear components are helpful for discriminating between groups of samples, e.g., mutant and wild-type. However, in the case of continuously observed factors such as time series, the data show usually a nonlinear behaviour and hence can be better explained by a curve. |
PCA transformation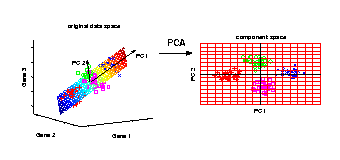
[ pdf | gif | png | eps ] |
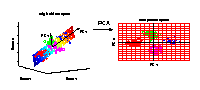
Illustrated is the transformation of PCA which reduces a large
number of variables (genes) to a lower number of new variables
termed principal components (PCs).
Three-dimensional gene expression samples are projected onto
a two dimensional component space that maintains the largest
variance in the data.
This two-dimensional visualisation of the samples allows
us to make qualitative conclusions about the separability
of our four experimental conditions.
|
The generative model of ICA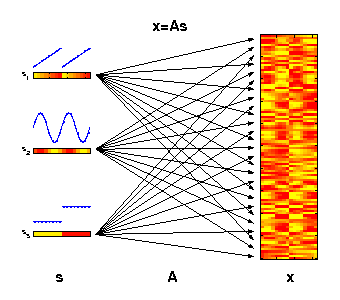
[ pdf | gif | png | eps ] |
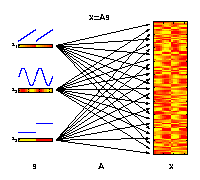
The motivation for applying ICA is that the measured molecular data
can be considered as derived from a set of experimental factors s.
This may include internal biological factors as well as external
environmental or technical factors. Each observed variable
x (e.g., gene)
can therefore be seen as a specific combination of these factors.
The illustrated factors may represent an increase of temperature
(s1),
an internal circadian rhythm
(s2), and different ecotypes
(s3).
|
ICA versus PCA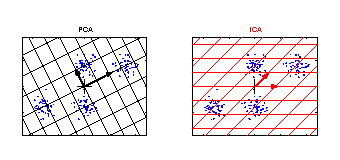
[ pdf | gif | png | eps ] |
PCA and ICA applied to an artificial data set. The grid represents the new coordinate system after PCA or ICA transformation. The identified components are marked by an arrow. The components of ICA are related better to the cluster structure of the data. They have an independent meaning. One component of ICA contains information to separate the clusters above from the clusters below, whereas the other component can be used to discriminate the cluster on the left from the cluster on the right. |
Kurtosis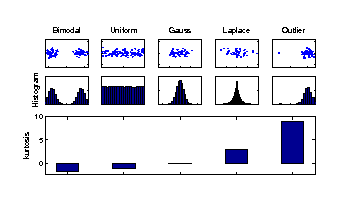
[ pdf | gif | png | eps ] |
Kurtosis is used to measure the deviation of a particular component distribution from a Gaussian distribution. The kurtosis of a Gaussian distribution is zero (middle), of super-Gaussian distributions positive (right), and of sub-Gaussian distributions negative (left). Sub-Gaussian distributions can point out bimodal structures from different experimental conditions or uniformly distributed factors such as a constant change in temperature. Thus the components of most negative kurtosis provide the most important information in molecular data. |
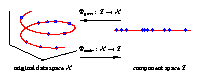
Nonlinear dimensionality reduction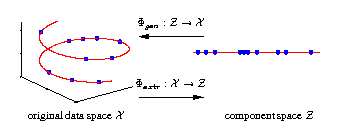
[ pdf | gif | png | eps ] |
Illustrated are three-dimensional samples that are located on
a one-dimensional subspace, and hence can be described without
loss of information by a single variable (the component).
The transformation is given by the two functions
Φextr
and
Φgen.
The extraction function
Φextr
maps each three-dimensional
sample vector (left) onto a one-dimensional component value (right).
The inverse mapping is given by the generation function
Φgen
which transforms any scalar component value back into the
original data space.
|
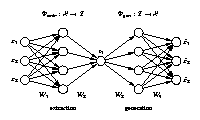
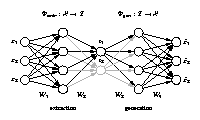
Standard auto-associative neural network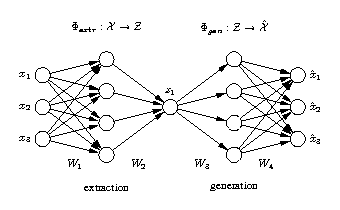
[ pdf | gif | png | eps ] |
The network output x is required to be equal to the input x. Illustrated is a [3-4-1-4-3] network architecture. Biases have been omitted for clarity. Three-dimensional samples x are compressed (projected) to one component z in the middle by the extraction part. The inverse generation part reconstructs x from z. The output is usually a noise-reduced representation of the input. The second and fourth hidden layer, with four nonlinear units each, enable the network to perform nonlinear mappings. The network can be extended to extract more than one component by using additional nodes in the component layer in the middle. |
Hierarchical auto-associative neural network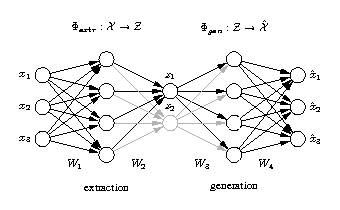
[ pdf | gif | png | eps ] |
The standard auto-associative network is hierarchically extended to perform a hierarchical NLPCA (h-NLPCA). In addition to the whole [3-4-2-4-3] network (grey+black), there is a [3-4-1-4-3] subnetwork (black) explicitly considered. The component layer in the middle has either one or two nodes which represent the first and second components respectively. In each iteration the error E1 of the subnetwork with one component and the error of the total network with two components are estimated separately. The network weights are then adapted jointly with regard to the total hierarchic error E=E1+ E1,2. |
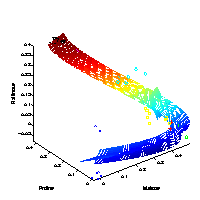
Hierarchical nonlinear PCA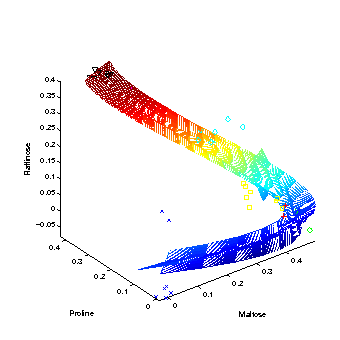
[ pdf | gif | png | eps ] |
The first three extracted nonlinear components are plotted into the data space, given by the top three metabolites of highest variance. The grid represents the new coordinate system after the nonlinear transformation. The principal curvature, the first nonlinear component, shows the trajectory over time in the cold stress experiment. The additional second and third component only represent the noise in the data. |
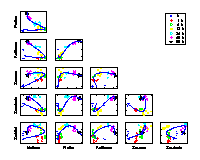
Time trajectory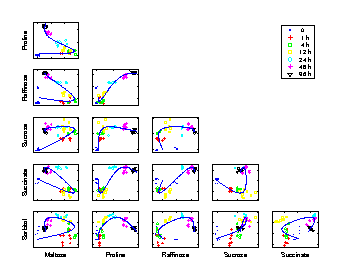
[ pdf | gif | png | eps ] |
Scatter plots of pair-wise metabolite combinations of six selected metabolites of highest relative variance. The extracted time component (nonlinear PC 1) is marked by a curve, which shows a strong nonlinear behaviour. |
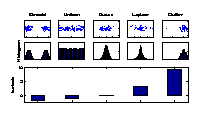
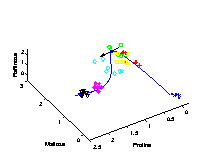
Identifying candidate molecules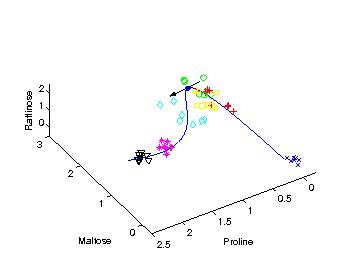
[ pdf | gif | png | eps ] |
The tangent (black arrow) on the curved time component
provides the direction
of change in molecular composition at the particular time
corresponding to the position on the curve.
The most important metabolites, those with highest relative change
on their concentration levels, are given by the closest angle
between any of the axes representing the metabolites and the
direction of the tangent.
|